What Are Pigments? And what (and why) is color?
What are pigments? At Ancient Earth Pigments, we deal with pigments as powdered solids that are used as the coloring agents of paints or for other color-conferring purposes. But what is the origin of the colors pigments exhibit? A more scientific and general definition of a pigment is a substance that selectively absorbs light in the visible waveband. When you illuminate something containing a pigment with light, some is absorbed, some might pass through, and some of the light bounces back to your eyeballs. It is the selective nature of the absorption that gives rise to what we perceive as color: a pigment that absorbs all colors of light equally will look gray (or black), when illuminated by white light. If a pigment absorbs blue light, it could look yellow or red, because those colors are not absorbed. If it absorbs red light it could look blue, or blue-green. When you mix colored paints, you combine the absorption properties of the different pigments to yield new colors. White pigments are a special case – they don’t selectively absorb colors, in fact they reflect light very efficiently without absorption, which is why they will lighten color mixes – returning more white light to your eyes.
The color of the ocean (title picture) serves to highlight this well. Pure water is blue, because it absorbs red light. If you add plants to the water, it looks more green. The ocean near tropical beaches have a bright turqoise color because the blue color is modulated by the calcium carbonate white sand suspended in the water.

A blue pigment absorbs red, orange, green 
A green pigment absorbs, red, orange, blue 
A white pigment absorbs little but reflects much
But how do pigments work, and what is absorption of light, really? To understand this it helps to think of light – or electromagnetic energy in general – as a stream of individual photons, where each photon is a little packet of energy. Each photon has a characteristic energy level, which correlates to its color. Blue or violet photons have higher energy then green, yellow, orange, or red photons, which in turn have more energy than infrared, microwave, or radio photons. Ultraviolet photons (and x-rays and gamma rays) have more energy than blue photons. If a chemical compound has a particular arrangement of its electrons that has a characteristic energy level that exactly matches a photon that encounters this compound in space/time, the photon can be absorbed. This means its energy goes into the chemical compound, and the compound gets excited, and this excitation can result in some work being done. Usually this just means the compound moves around a bit more – it heats up, basically – but in the case of what we call visible light (violet to red, on the energy spectrum), it can slightly rearrange chemical bonds, changing the shape of (for example) one of the pigments in a cone or rod cell in your retina. And that shape change stimulates a nerve impulse, telling your brain that (for example) a blue photon just went through your eye.
Infrared light is too weak to rearrange this bond, so we can’t see it, but we can perceive the heat energy that it can transfer. Ultraviolet light also does not rearrange bonds in the proper way – in fact it can break them altogether, or cause other undesirable chemical reactions, which is why ultraviolet light and X-rays and gamma rays are dangerous, even though we can’t see them.
But what are pigments, chemically? The particular arrangements of electrons that result in color in chemical compounds can be found in several different types of compounds: metal coordination complexes, organometallic compounds, and organic compounds. You probably already know that metals play important roles in pigments, but in pure metallic form, metals are generally shiny and reflective and don’t have much if any color. However, ions of metals are very reactive, and play important roles in biochemistry and geochemistry, and can in many cases make for brilliant colors. In some cases the color itself plays an important role.
Coordination complexes are individual metal atoms, in a particular ionic state, that are surrounded by other ions or molecules in a characteristic arrangement. The ionization state of the metal atom and the number and kind of the molecules bound to it all control the absorption properties of the complex, so the same metal can give rise to many different dramatic colors. The following table shows some examples of coordination complexes of iron (in two different ionization states), cobalt (Co), copper (Cu), aluminum (Al), and chromium (Cr). Many of these colors are found in familiar pigments.
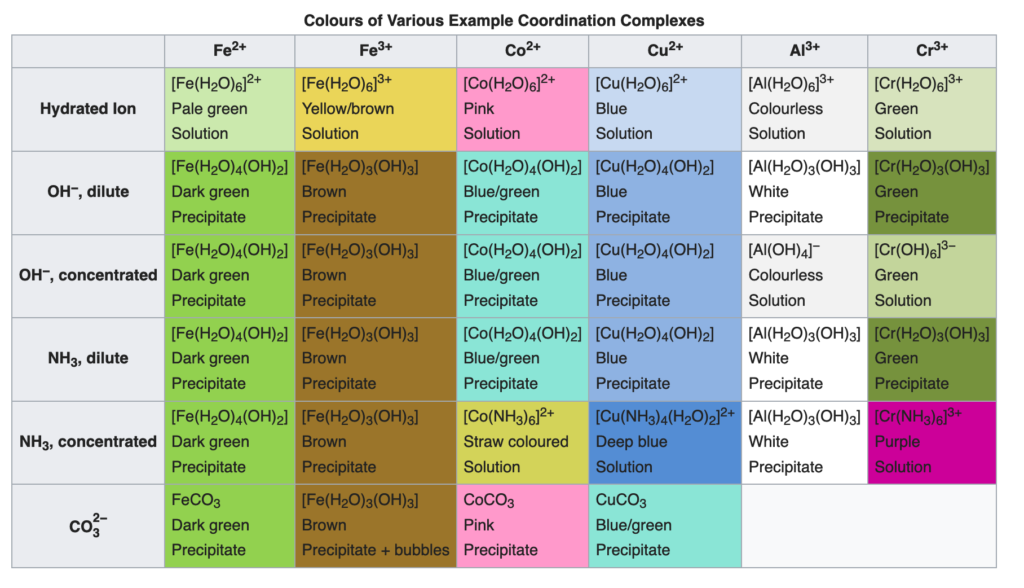
https://en.wikipedia.org/wiki/Coordination_complex
Coordination complexes often occur in natural minerals. Natural ‘earth’ pigments from mineral soils have red and brown colors that most often come from oxidized iron (Fe3+) complexed with water (H2O) or hydroxides (OH) yielding different shades depending on the exact combination of waters and/or hydroxides. These kinds of colors can be quite stable, which is why they have been used for over ten thousand years as pigments for painting and dyeing.
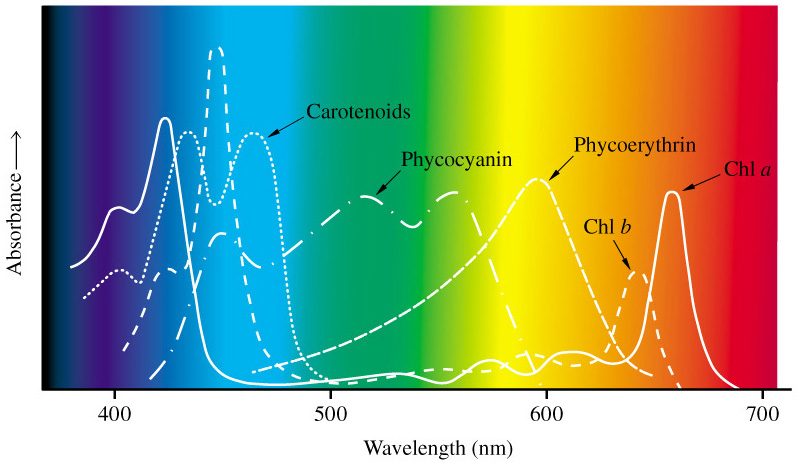
Organometallic compounds are a bit fancier but they rarely make good pigments because they are unstable and break down easily, resulting in disappointingly gray colors. They consist of a metal ion that has been chelated (bound up) by an organic molecule. A famous example of this is chlorophyll, in which a ring of carbon and nitrogen atoms surrounds a magnesium ion. Chlorophyll famously has two strong absorption bands in the red and the blue (see above figure), giving rise to the green color of plants.
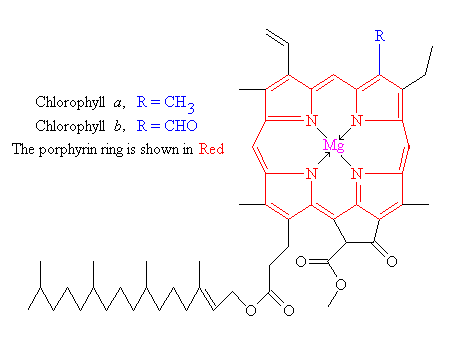
Another famous example of an organometallic compound is heme, which the red-colored part of the oxygen-carrying protein in blood called hemoglobin. Heme consists of the same ring (red in the chlorophyll figure) only with an iron instead of a magnesium ion at the center. Both chlorophyll a and hemoglobin have amazing biological roles. Chlorophyll a molecules, when they absorb light energy in the blue or red wavebands, can ionize – give up an electron – the first step in photosynthesis. Hemoglobin, of course, selectively grabs onto oxygen molecules when they are abundant and gives them up when they are rare, making it the transporter of oxygen from your lungs to the far-flung parts of your body that need it. Unfortunately, organometals, while they are the spiffiest of biological pigments, do not make good painting colors as a rule.
The last category of pigments are the ones that are purely organic – meaning they consist only of carbon, nitrogen, oxygen, and hydrogen, no metals. These compounds achieve the same sorts of electronic arrangements as coordination complexes or organometals by conjugating lots of alternating single and double bonds between carbon atoms (don’t worry about this). Some of these are natural products, but many that we use are synthetic, produced in the laboratory or factory to be pigments and dyes. Some familiar pigments are the carotenoids that are found in colorful vegetables (orange in carrots is mostly beta-carotene, an organic compound), and the anthocyanins found in flowers. Indigo, an important pigment and dye, is an organic pigment derived from amino acids – but it can also be produced synthetically. Cochineal crimson, produced by South American bugs, is also an organic compound. The famous Tyrian purple is an indigo derivative produced by a marine snail. Many synthetic pigments, such as alizarin and azo dyes, are organic compounds similar to some natural products. In many cases, however, the natural pigments have different properties because of the presence of natural impurities or precursors or other pigments in the mix.
Some familiar organic pigments found in dyes, such as madder, don’t make good painting pigment powders unless they are treated with other chemicals (such as alum or calcium carbonate from chalk or bone) to make them precipitate into solids. This process results in lake pigments, and one form or another has been used for pigments and for dyeing since prehistory. In modern times lake pigments made from natural products have mostly been replaced by less-fugitive synthetic colors.

Titian used rose madder lake in the crimson robes.
You don’t always need this knowledge of physics and chemistry to effectively use pigments in your artwork. However, it is kind of fun to understand some of the background behind the material you use, and some of the information may come in handy at some point. If you have questions, please make a comment and I will respond.
Thank you for joining us as we do Pandemic Projects, meant to keep you energized, curious and learning!

[…] conjugated bonds, with some stuff at either end. Rings are frequently found in these structures. In The Science of Pigments we talked about the porphyrin rings that bind up metal ions to make chlorophyll or heme (found in […]
[…] is frequently a colorless metal salt that can form a coordination complex (as described in our earlier article) with the organic dye molecule and still have the ability to bind with something else. In the case […]